オムニホイールについて
オムニホイールは,上の動画のマシンに搭載されているような駆動輪で,ホイールの駆動方向と垂直な方向に対して自由に滑るようになっている.
(2017/06/04 追記)
本記事のロボットで使用したオムニホイールは オムニホイールの購入に関するメモ で紹介したKornylak社のFXAシリーズであるが,送料等を考えると2017年6月現在ではVstoneのなめらかオムニホイールがおすすめである.
概要
オムニホイールを利用して,車体角度を変えずに(もしくは自由に変えながら)全方向に移動することができる全方向移動車の作成をするとともに,この特殊な車輪に関する性質や制御の方法について学ぶ.
計算
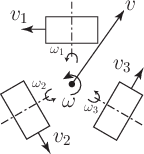
はじめに,機体座標系 \((x,y)\) で見たとき,無回転で速度ベクトル \((v_x,v_y)\) にしたがって移動する場合について考える.オムニホイールは軸に垂直な方向にすべるため,それを考慮して条件を導出し,ホイールそれぞれの回転する速さ \(v_i\) を \((v_x,v_y)\) で表すことにしよう.
$$
v_1 = -v_x\\
v_2 = \frac{1}{2}v_x - \frac{\sqrt{3}}{2}v_y\\
v_3 = \frac{1}{2}v_x + \frac{\sqrt{3}}{2}v_y
$$
行列で表すと,
$$
\begin{bmatrix}
v_1\\
v_2\\
v_3
\end{bmatrix}
=
\begin{bmatrix}
-1 & 0\\
\frac{1}{2} & -\frac{\sqrt{3}}{2}\\
\frac{1}{2} & \frac{\sqrt{3}}{2}
\end{bmatrix}
\begin{bmatrix}
v_x\\
v_y
\end{bmatrix}
$$
となり,さらに回転を考慮すると,機体の角速度を \(\omega\) ,機体中心からホイールまでの距離を \(r\) として,
$$
\begin{bmatrix}
v_1\\
v_2\\
v_3
\end{bmatrix}
=
\begin{bmatrix}
-1 & 0 & r\\
\frac{1}{2} & -\frac{\sqrt{3}}{2} & r\\
\frac{1}{2} & \frac{\sqrt{3}}{2} & r
\end{bmatrix}
\begin{bmatrix}
v_x\\
v_y\\
\omega
\end{bmatrix}
$$
と表すことができる.
次に,機体座標系からフィールド座標系への変換を考える.機体の角度 \(\theta^{\ast}=\int{\omega dt}\) ,フィールド座標系での速度ベクトル \((v_x^{\ast},v_y^{\ast})\) として, \(v_i\) をこれらを用いて表すことを考えよう.
いま,一例として \(v_x^{\ast},v_y^{\ast},\omega\) が全て一定値を取る場合を考える.
機体が \(\theta^{\ast}\) だけ斜めになっているとき,機体座標系での \((v_x,v_y)\) を \((v_x^{\ast},v_y^{\ast})\) で表すと,
$$
\begin{bmatrix}
v_x\\
v_y
\end{bmatrix}
=R(-\theta^\ast)
\begin{bmatrix}
v_x^\ast\\
v_y^\ast
\end{bmatrix}
=
\begin{bmatrix}
\cos\theta^\ast & \sin\theta^\ast\\
-\sin\theta^\ast & \cos\theta^\ast
\end{bmatrix}
\begin{bmatrix}
v_x^\ast\\
v_y^\ast
\end{bmatrix}
=
\begin{bmatrix}
v_x^\ast\cos\theta^\ast+v_y^\ast\sin\theta^\ast\\
-v_x^\ast\sin\theta^\ast+v_y^\ast\cos\theta^\ast
:q
\end{bmatrix}
$$
これをはじめの式に代入して \(v_i\) による表示にすると, \begin{align*} \begin{bmatrix} v_1\\ v_2\\ v_3 \end{bmatrix} &= \begin{bmatrix} -1 & 0 & r\\ \frac{1}{2} & -\frac{\sqrt{3}}{2} & r\\ \frac{1}{2} & \frac{\sqrt{3}}{2} & r \end{bmatrix} \begin{bmatrix} v_x^\ast\cos\theta^\ast+v_y^\ast\sin\theta^\ast\\ -v_x^\ast\sin\theta^\ast+v_y^\ast\cos\theta^\ast\\ \omega \end{bmatrix}\\ &= \begin{bmatrix} -v_x^\ast\cos\theta^\ast-v_y^\ast\sin\theta^\ast+r\omega\\ -v_x^\ast\cos\left(\theta^\ast+\frac{2}{3}\pi\right)+v_y^\ast\sin\left(\theta^\ast+\frac{2}{3}\pi\right)+r\omega\\ v_x^\ast\cos\left(\theta^\ast+\frac{\pi}{3}\right)+v_y^\ast\sin\left(\theta^\ast+\frac{\pi}{3}\right)+r\omega \end{bmatrix} \end{align*}
という結果が得られる.
それぞれ \(v_x^{\ast},v_y^{\ast},\omega\) のパラメータを設定することで,角速度 \(\omega\) で回転しながら速度ベクトル \((v_x^{\ast},v_y^{\ast})\) にしたがって運動させることができる(はず).
これはあくまでフィードフォワード的なお話.
製作
6/25 設計開始
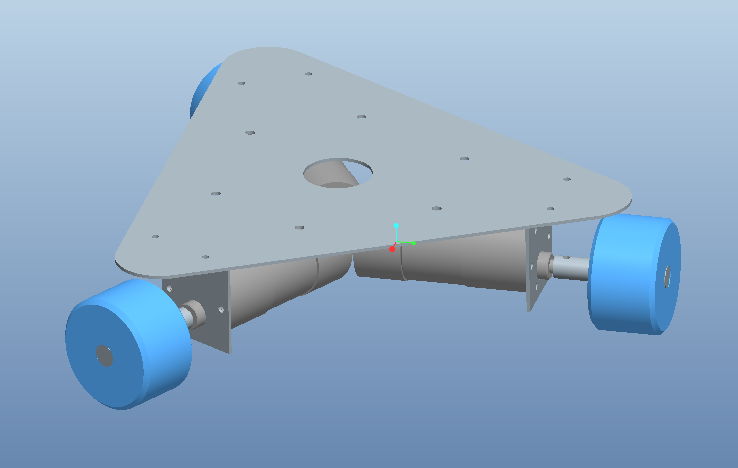
オムニホイールを使用する部分については設計がほぼ完了.
作業時間:4時間 今週小計:4時間 製作合計:4時間
6/26 軸部品試作

作業時間:3.5時間 今週小計:7.5時間 製作合計:7.5時間
8/8 軸部品作成,板材加工
作業時間:2.5時間 今週小計:2.5時間 製作合計:10時間
8/9 板材加工
作業時間:3時間 今週小計:5.5時間 製作合計:13時間
8/10 仮組み

作業時間:2時間 今週小計:7.5時間 製作合計:15時間
8/20〜プログラミング開始
STM32F10x向けに開発を開始.
実装内容
- USART(通信のため)
- PWM(モータのため)
- EXTI(エンコーダのため)
- (
printfデバッグのため これを入れるとバイナリが膨れ上がる)
作業時間:20時間 今週小計:20時間 製作合計:35時間
8/26 電源基板換装,基板固定
3端子レギュレータでは発熱がひどいため,DCDCコンバータを利用して11.1Vから5Vを作ることにした.

作業時間:2時間 今週小計:2時間 製作合計:37時間
8/27 角度計算の見直し
補正係数が必要になった.ぐぬぬ
作業時間:4時間
今週小計:4時間
製作合計:41時間
8/28 コマンド通信の実装
BluetoothシリアルモジュールにつながっているUSARTに対して所定の形式のコマンドを叩くことで,速度ベクトルや角速度ベクトルを更新することができるようにした.
コマンドの形式:
[開始コード 0x02] [コマンド番号 0x10-0x1F] [データ 4bytes] [チェックサム] [終了コード 0x03] |
データにはfloatやlongの値が入るようになっている.
作業時間:3時間 今週小計:7時間 製作合計:44時間
8/29〜9/1 Androidアプリの開発
実装したコマンド通信を利用して,Androidアプリ上からマシンをラジコン的に操作できるようにする作業をおこなった.
アナログパッド風のコントロールがデフォルトでなかったため,ImageViewを継承してAnalogPadクラスを作成した.
Bluetoothによる通信は,AndroidSDKの「BluetoothChat」というサンプルをベースにして作成した.
UI等詰め切れていないため今後改善予定.
作業時間:15時間 今週小計:22時間 製作合計:59時間
9/2〜9/5 フィードバックの見直しとD制御の実装
作業時間:12時間 今週小計:12時間 製作合計:71時間