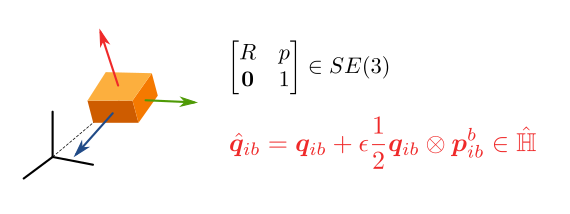
概要
クォータニオンを拡張した概念として, Dual Quaternionというものがあります. これを使うと, クォータニオンで考えられる3次元の回転に加えて, 3次元の並進まで1つの枠組みで考えることができるというすぐれもので, ロボティクスやCGの分野でほそぼそと使われています.
今回はDual Quaternionの基礎と, 3次元の位置・姿勢のDual Quaternion表現, そして剛体の運動をDual Quaternionで記述する方法について書きます.
若干偏った事前知識が必要かもしれません. 誤り等があればまさかりを投げてください.
準備
クォータニオン(Quaternion)
クォータニオン(quaternion)は,
クォータニオンはつぎの規則を満たす基底 $1, i, j, k$ をもつ数 $a + bi + cj + dk$ です. $$ i^2 = j^2 = k^2 = ijk = -1 $$ 複素数の次元を拡張したような形をしています. クォータニオンは実数と3次元実ベクトルの組として表記されることが多いため, この記事でもその記法を使用することにします. $$ \boldsymbol q = (q_0, \boldsymbol{q}_v) = (a, [b\ c\ d]^T) $$
Dual Quaternionの定義のために, 集合をいくつか定義しておきます[1].
| 定義 | 説明 |
|---|---|
| $\mathbb{H} = \{(q_0, \boldsymbol{q}_v) \mid q_0 \in \mathbb{R}, \boldsymbol{q}_v \in \mathbb{R}^3\}$ | クォータニオン全体の集合 |
| $\mathbb{H}_u = \{ \boldsymbol q \in \mathbb{H} \mid \lVert \boldsymbol q \rVert = 1 \}$ | 単位クォータニオン全体の集合 |
| $\mathbb{H}_v = \{\boldsymbol q \in \mathbb{H} \mid q_0 = 0\}$ | ベクトルクォータニオン全体の集合 |
クォータニオンを用いて回転を表現するには, 大きさが1の単位クォータニオンであることが重要です(詳しくは後述).
ベクトルクォータニオンは, スカラー部分が0でベクトル部分にのみ値を持つクォータニオンのことを指します. クォータニオンからベクトルクォータニオンを取り出す(スカラー部分を0にする)演算子を $\mathrm{vec}(\cdot)$ と表記します.
クォータニオンの基本演算
和・差
$ \boldsymbol q_1 \pm \boldsymbol q_2 = (q_{1,0} \pm q_{2,0},\ \boldsymbol q_{1,v} \pm \boldsymbol q_{2,v})$
内積
$ \boldsymbol q_1 \cdot \boldsymbol q_2 = q_{1,0}q_{2,0} + \boldsymbol q_{1,v} \cdot \boldsymbol q_{2,v}$
外積
$ \boldsymbol q_1 \times \boldsymbol q_2 = (0,\ q_{1,0}\boldsymbol q_{2,v} + q_{2,0}\boldsymbol q_{1,v} + \boldsymbol q_{1,v} \times \boldsymbol q_{2,v})$
クォータニオン積
$ \boldsymbol q_1 \otimes \boldsymbol q_2 = (q_{1,0}q_{2,0} - \boldsymbol q_{1,v} \cdot \boldsymbol q_{2,v},\ q_{1,0}\boldsymbol q_{2,v} + q_{2,0}\boldsymbol q_{1,v} + \boldsymbol q_{1,v} \times \boldsymbol q_{2,v})$
共役
$\boldsymbol q^\ast = (q_0, -\boldsymbol q_v)$
ノルム
$ \lVert \boldsymbol q \rVert = \sqrt{\boldsymbol q \cdot \boldsymbol q} = \sqrt{\boldsymbol q \otimes \boldsymbol q^\ast} = \sqrt{\boldsymbol q^\ast \otimes \boldsymbol q} = \sqrt{q_0^2 + \lVert\boldsymbol q_v\rVert^2}$
単位元
$\boldsymbol q_I = (1, [0\ 0\ 0]^T)$ に対して
$$
\boldsymbol q_I \otimes \boldsymbol q = \boldsymbol q \otimes \boldsymbol q_I = \boldsymbol q\\
\boldsymbol q^\ast \otimes \boldsymbol q = \boldsymbol q \otimes \boldsymbol q^\ast = \lVert \boldsymbol q \rVert^2\boldsymbol q_I
$$
回転変換としての単位クォータニオン
単位円上の複素数は2次元の回転変換(と姿勢)を表わすことができますが, 単位クォータニオンは3次元の回転変換(と姿勢)を表現できます. 回転角を $\theta \in \mathbb{R}$, 回転軸を $\boldsymbol\xi \in \mathbb{R}^3$ とするとき, $$ \boldsymbol q = (\cos\frac\theta2, \boldsymbol\xi \sin\frac\theta2) $$ によって回転を表現できます.
点の位置ベクトルを表すベクトルクォータニオン $\boldsymbol p = (0, \boldsymbol p_v)$ を $\boldsymbol q$ によって移すには, $\boldsymbol q \otimes \boldsymbol p \otimes \boldsymbol q^\ast$ というクォータニオン積を考えます.
符号違いの2つの単位クォータニオン $\pm \boldsymbol q$ が同一の回転を表すことに注意してください. $-\boldsymbol q$ は, $\boldsymbol q$ の回転軸軸ベクトル $\xi$ を逆向きにして $2\pi-\theta$ つまり $-\theta$ 回転させることを表していて, この回転はもとの $\boldsymbol q$ による回転と等価になります. また, 大きさが1であるということは, 変換の際に相手の大きさを変えないという性質を表しています.
二重数 (Dual Number)
二重数(dual number)はざっくり言うと複素数の別のバリエーションのようなもの[2]です. $\epsilon \neq 0, \epsilon^2 = 0$ となるような新しい基底を持ってきて $a + \epsilon b$ としたものが二重数です.
ちなみに二重数は行列を使って表すことができます [3]. $$ a + \epsilon b : \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}a + \begin{bmatrix} 0& 1\\ 0 &0 \end{bmatrix}b $$ コンピュータで数値計算を行う際には, この表現が便利になることがあるらしいです.
自動微分[4]という面白い用途もあるようです.
DQ(Dual Quaternion)の基礎
ようやく本題です. Dual Quaernion(二重クォータニオン, 二重四元数)は, 二重数とクォータニオンをあわせたものです. $$ \hat{\boldsymbol q} = \boldsymbol q_p + \epsilon \boldsymbol q_d $$ ただし, $\boldsymbol q_p, \boldsymbol q_d \in \mathbb{H}$ で, $\boldsymbol q_p$ は primary part, $\boldsymbol q_d$ は dual part と呼ばれます.
| 定義 | 説明 |
|---|---|
| $\hat{\mathbb{H}} = \{ \boldsymbol q_p + \epsilon \boldsymbol q_d \mid \boldsymbol q_p, \boldsymbol q_d \in \mathbb{H}\}$ | DQ全体の集合 |
| $\hat{\mathbb{H}}_u = \{ \hat{\boldsymbol q} \in \hat{\mathbb{H}} \mid \boldsymbol q_p \in \mathbb{H}_u, \boldsymbol q_p \otimes \boldsymbol q_d^\ast + \boldsymbol q_d \otimes \boldsymbol q_p^\ast = 0 \}$ | 単位DQ全体の集合 |
| $\hat{\mathbb{H}}_v = \{\boldsymbol q \in \hat{\mathbb{H}} \mid \boldsymbol q_p, \boldsymbol q_d \in \mathbb{H}_v \}$ | ベクトルDQ全体の集合 |
単位DQのdual partにはノルムに関する制約がなく, 代わりにprimary partとdual partの可換性に関する条件が加わっています(ノルム1とは限らないということに注意してください).
あとで説明しますが, primary partで回転, dual partで並進に関する部分を表現できるようになり, 剛体の3次元位置・姿勢がDQの枠組みで扱えるようになります.
DQの基本演算
和・差
$ \hat{\boldsymbol q}_1 \pm \hat{\boldsymbol q}_2 = \boldsymbol q_{1,p} \pm \boldsymbol q_{2,p} + \epsilon (\boldsymbol q_{1,d} \pm \boldsymbol q_{2,d}) $
内積・ノルム
$ \hat{\boldsymbol q}_1 \cdot \hat{\boldsymbol q}_2 = \boldsymbol q_{1,p} \cdot \boldsymbol q_{2,p} + \boldsymbol q_{1,d} \cdot \boldsymbol q_{2,d}$
外積
$ \hat{\boldsymbol q}_1 \times \hat{\boldsymbol q}_2 = \boldsymbol q_{1,p} \times \boldsymbol q_{2,p} + \epsilon (\boldsymbol q_{1,p}\times \boldsymbol q_{2,d} + \boldsymbol q_{1,d} \times \boldsymbol q_{2,p})$
クォータニオン積
$ \hat{\boldsymbol q}_1 \otimes \hat{\boldsymbol q}_2 = \boldsymbol q_{1,p} \otimes \boldsymbol q_{2,p} + \epsilon (\boldsymbol q_{1,p}\otimes \boldsymbol q_{2,d} + \boldsymbol q_{1,d} \otimes \boldsymbol q_{2,p})$
共役
- $\hat{\boldsymbol q}^\ast = \boldsymbol q_p^\ast + \epsilon \boldsymbol q_d^\ast$
- $\bar{\hat{\boldsymbol q}} = \boldsymbol q_p - \epsilon \boldsymbol q_d$
単位元
$\hat{\boldsymbol q}_I = \boldsymbol q_I + \epsilon \boldsymbol 0$ に対して
$$
\hat{\boldsymbol q}_I \otimes \hat{\boldsymbol q} = \hat{\boldsymbol q} \otimes \hat{\boldsymbol q}_I = \hat{\boldsymbol q}\\
\hat{\boldsymbol q}^\ast \otimes \hat{\boldsymbol q} = \hat{\boldsymbol q} \otimes \hat{\boldsymbol q}^\ast = \lVert\hat{\boldsymbol q}\rVert^2\hat{\boldsymbol q}_I
$$
剛体の位置・姿勢の表現
さて, これでツールがようやく揃ったので, ここからは3次元空間上の剛体の運動をDQを用いて記述していきます.
運動を考える前に, まずはDQで剛体の位置・姿勢を表現します. ワールドに固定された座標系(慣性座標系)を $\Sigma_i$, 剛体に固定された座標系(ボディ座標系)を $\Sigma_b$ とします. 慣性座標系からみたボディ座標系の姿勢を表すクォータニオンを $\boldsymbol q_{ib} \in \mathbb{H}_u$ , 慣性座標系から見たボディ座標系の原点の位置をクォータニオン $\boldsymbol p^i_{ib} \in \mathbb{H}_v$ を用いて表します. このとき, 剛体の位置・姿勢は $$ \hat{\boldsymbol q}_{ib} = \boldsymbol q_{ib} + \epsilon \frac12 \boldsymbol p^i_{ib} \otimes \boldsymbol q_{ib} $$ と書けます. また, ボディ座標系を基準に慣性座標系の原点からの位置ベクトル $\boldsymbol p^b_{ib}$ を取ることもできて, その場合以下のような式になります. $$ \hat{\boldsymbol q}_{ib} = \boldsymbol q_{ib} + \epsilon \frac12 \boldsymbol q_{ib} \otimes \boldsymbol p^b_{ib} $$
$\boldsymbol p^i_{ib}$ と $\boldsymbol p^b_{ib}$ は意味が異なり, 一般に等しくならないことに注意が必要です. これらの間には以下の等式が成り立ちます. $$ \boldsymbol p^i_{ib} \otimes \boldsymbol q_{ib} = \boldsymbol q_{ib} \otimes \boldsymbol p^b_{ib} $$ この等式を用いることで $\boldsymbol p^i_{ib}$ と $\boldsymbol p^b_{ib}$ との間を行き来できます.
なぜこうなるのか(説明が下手なので読み飛ばしてOK)
上記の式では, 剛体の位置があまり自明ではない形でdual partに格納されています. この位置・姿勢表現は, 純粋な並進と純粋な回転を表す2つのDQを合成したDQとして定義されています.
回転せずに $\boldsymbol p_{ib}$ だけ並進移動するDQは以下のようになります. $$ \hat{\boldsymbol q}_L = \boldsymbol q_I + \epsilon \frac12 \boldsymbol p_{ib} $$ 同様に, 回転 $\boldsymbol q_{ib}$ しかしないDQは以下のようになります. $$ \hat{\boldsymbol q}_A = \boldsymbol q_{ib} + \epsilon \boldsymbol 0 $$
慣性座標系でボディ座標系を回転させてから, 慣性座標系でボディ座標系の原点を並進移動する変換[5]は, $$ \hat{\boldsymbol q}_L \otimes \hat{\boldsymbol q}_A = \boldsymbol q_{ib} + \epsilon \frac12 \boldsymbol p_{ib} \otimes \boldsymbol q_{ib} $$ と計算できます[6]. このときの $\boldsymbol p_{ib}$ は, 慣性座標系で表現されたボディ座標系の原点の位置 $\boldsymbol p^i_{ib}$ に相当します.
同様に, 慣性座標系でボディ座標系の原点を並進移動させてから, 慣性座標系でボディ座標系を回転する変換[7]は, $$ \hat{\boldsymbol q}_A \otimes \hat{\boldsymbol q}_L = \boldsymbol q_{ib} + \epsilon \frac12 \boldsymbol q_{ib} \otimes \boldsymbol p_{ib} $$ と計算でき, このときの $\boldsymbol p_{ib}$ は, ボディ座標系で見た「慣性座標系の原点からボディ座標系の原点へのベクトル」$\boldsymbol p^b_{ib}$に相当します.
…なにやらややこしいですね. 変換が可換ではないので, どうしてもこのようなややこしさが生じてしまいます.
ここで確認したように, $\boldsymbol p^i_{ib}$ と $\boldsymbol p^b_{ib}$ はそれぞれ違うものを指し示しています. したがって, 混同してしまうと座標を正しく表現することができなくなります. $\boldsymbol p^i_{ib}$ が物理的にわかりやすいのですが, 後述するように, こちらを採用すると今度は角速度がわかりづらくなります.
運動学(キネマティクス)
クォータニオンと角速度
まずは回転のみに着目してみます. 剛体の姿勢を表す単位クォータニオン $\boldsymbol q_{ib} \in \mathbb{H}_u$ の時間微分は, ボディ角速度ベクトルを表すクォータニオン $\boldsymbol \omega^b \in \mathbb{H}_v$ を用いて $$ \dot{\boldsymbol q}_{ib} = \frac12 \boldsymbol q_{ib} \otimes \boldsymbol \omega^b $$ と書けることが知られています[8].
オイラー角やロール・ピッチ・ヨー角を使用した姿勢表現の場合, 姿勢角の時間微分と角速度ベクトルとの間の変換が必要になりますが, クォータニオンを使えば現在の姿勢と角速度ベクトルのクォータニオン積という非常にシンプルな形で時間微分を書くことができます. しかも, 冒頭で説明したような特異点の問題もありません.
また, 別の角速度(空間角速度, spatial angular velocity)を使って $$ \dot{\boldsymbol q}_{ib} = \frac12 \boldsymbol \omega^i \otimes \boldsymbol q_{ib} $$ と書くこともできます.
機体に搭載するジャイロセンサで計測できるのはボディ角速度 $\boldsymbol \omega^b$ です. 実用を考えると, 後者の式は少し使いづらくなります. 空間角速度とボディ角速度の間には以下の関係が成り立つので, これを利用することで行き来することができます. $$ \boldsymbol \omega^i \otimes \boldsymbol q_{ib} = \boldsymbol q_{ib} \otimes \boldsymbol \omega^b $$ この式は, 先述した $\boldsymbol p^i, \boldsymbol p^b$ に関する式とも対応しています.
DQの時間微分
DQの時間微分もクォータニオンの時間微分と対応づいた形で書くことができます. DQにおける速度に対応する $\hat{\boldsymbol\omega}$ のことを, Dual Velocity と呼びます.
ボディ速度(body velocity)のベクトルクォータニオンを $\boldsymbol v^b = \dot{\boldsymbol p}^b_{ib} + \boldsymbol \omega^b \times \boldsymbol p^b_{ib} \in \mathbb{H}_v$ と定義します[9]. 泥臭く各成分を微分してきます. $$ \begin{align*} \dot{\hat{\boldsymbol q}}_{ib} &= \dot{\boldsymbol q}_{ib} + \epsilon \frac12\left( \dot{\boldsymbol q}_{ib} \otimes \boldsymbol p^b_{ib} + \boldsymbol q_{ib} \otimes \dot{\boldsymbol p}^b_{ib} \right)\\ &= \frac12 \boldsymbol q_{ib} \otimes \boldsymbol \omega^b + \epsilon \frac12\left( \frac12 \boldsymbol q_{ib} \otimes \boldsymbol \omega^b \otimes \boldsymbol p^b_{ib} + \boldsymbol q_{ib} \otimes \dot{\boldsymbol p}^b_{ib} \right)\\ &= \frac12 \boldsymbol q_{ib} \otimes \boldsymbol \omega^b + \epsilon \frac12\left( \frac12 \boldsymbol q_{ib} \otimes (\boldsymbol \omega^b \otimes \boldsymbol p^b_{ib} - 2 \boldsymbol \omega^b \times \boldsymbol p^b_{ib}) + \boldsymbol q_{ib} \otimes \boldsymbol v^b \right) \end{align*} $$ クォータニオン積の定義と, $\boldsymbol \omega^b, \boldsymbol p^b_{ib}$ がいずれもベクトルクォータニオンであることから, $\boldsymbol \omega^b \otimes \boldsymbol p^b_{ib} - 2 \boldsymbol \omega^b \times \boldsymbol p^b_{ib} = \boldsymbol p^b_{ib} \otimes \boldsymbol \omega^b$ が成り立つので, $$ \begin{align*} \dot{\hat{\boldsymbol q}}_{ib} &= \frac12 \boldsymbol q_{ib} \otimes \boldsymbol \omega^b + \epsilon \frac12\left( \frac12 \boldsymbol q_{ib} \otimes \boldsymbol p^b_{ib} \otimes \boldsymbol \omega^b + \boldsymbol q_{ib} \otimes \boldsymbol v^b \right)\\ &= \frac12 \hat{\boldsymbol q}_{ib} \otimes \hat{\boldsymbol\omega}^b \end{align*} $$ となります. ただし, $\hat{\boldsymbol\omega}^b = \boldsymbol \omega^b + \epsilon \boldsymbol v^b$ とおきました.
同様にして $$ \begin{align*} \dot{\hat{\boldsymbol q}}_{ib} &= \frac12 \hat{\boldsymbol\omega}^i \otimes \hat{\boldsymbol q}_{ib} \end{align*} $$ も言えるのですが, 先述したように空間角速度 $\boldsymbol\omega^i$ は解釈がしづらく, また, 並進成分である $\boldsymbol v^i$ も $\dot{\boldsymbol p}_{ib}^i$ ではなく, 角速度 $\boldsymbol \omega^i$ と干渉する形になるため, 物理的な解釈が難しくなります. ボディ速度と空間速度は, 単にみる座標系が異なるだけではなく, そのベクトルが意味する物理的な量も異なります. 詳しいことに関しては, 書籍[10]に詳しく書かれていますので, そちらを参照してください.
動力学(ダイナミクス)
回転行列の単純な2階微分に物理的な意味がないのと同様に, クォータニオンの2階微分には特に物理的に有用な意味はありません. 物理的に意味のある加速度・角加速度に対応するものは $\boldsymbol v, \boldsymbol \omega$ の時間微分で, これらが我々が扱うべきものです.
最も単純な運動方程式 $ma = F$ は, 運動量を $p = mv$ とすると, $$ \dot{p} = F $$ と書き直すことができます. これと同様の方法で, DQを使って並進と回転の運動量を定義し, そこから運動方程式を求めていきます.
運動量(Dual Momentum)
DQによる運動量(dual momentum)の定義の仕方には複数の流儀があるようなのですが, 本稿では文献[11]のものを採用します. $$ \hat{\boldsymbol h}^b = \hat M \hat{\boldsymbol \omega}^b = \boldsymbol h_L + \epsilon \boldsymbol h_A $$ $\boldsymbol h_L, \boldsymbol h_A$ は, それぞれ並進・回転の運動量です. $\hat M$ は慣性行列に対応する演算子(dual inertia operator)で, 以下の操作を行うものです. $$ \hat M \hat{\boldsymbol \omega}^b = \begin{bmatrix} 1 & \boldsymbol 0\\ \boldsymbol 0 & mI_3 \end{bmatrix} \boldsymbol v^b + \epsilon \begin{bmatrix} 1 & \boldsymbol 0\\ \boldsymbol 0 & J^b \end{bmatrix} \boldsymbol \omega^b $$ 若干記号を乱用していますが, $\boldsymbol v^b, \boldsymbol \omega^b$ のベクトル部にそれぞれ質量と慣性テンソルをかけて, primary partとdual partを入れ替える操作を表しています.
運動方程式
Dual momentumを使ってDQで運動方程式を記述すると, 以下のようになります. $$ \begin{align*} \dot{\hat{\boldsymbol h}}^b = \hat M \dot{\hat{\boldsymbol \omega}}^b &= \hat{\boldsymbol f}^b - \hat{\boldsymbol \omega}^b \times \hat M \hat{\boldsymbol \omega}^b\\ &= \underbrace{\hat{\boldsymbol f}^b_u}_{\text{印加力}} - \underbrace{\hat{\boldsymbol f}^b_G}_{\text{重力}} - \hat{\boldsymbol \omega}^b \times \hat M \hat{\boldsymbol \omega}^b \end{align*} $$ このように, 非常にコンパクトな形で運動方程式を書き表すことができます. 通常であれば, 以下のようになります. $$ M \begin{bmatrix} \dot{v}^b\\ \dot{\omega}^b \end{bmatrix} = f^b - \begin{bmatrix} m \omega^b \times v^b\\ \omega^b \times (J \omega^b) \end{bmatrix} $$ ……まあ, ほとんど変わらないわけですが, 遠心・コリオリ項がDQの演算によってぎゅっとまとまっただけでもありがたいものです.
また, ここまでで見てきたように演算はクォータニオンと対応する形になるので, 二重数の実装さえうまくできれば, 回転のみのコードから並進を含んだものへの移行は楽なのではないかと思います.
疑問点
Dual inertia operatorにおいて, primary partとdual partが入れ替わっているのは, 計算上は理解できるのですが, 何か物理的・幾何的な本質に関連しているのでしょうか? 何かご存知の方やピンときた方は教えてください.
記号の文字HはHamiltonの頭文字から来ています. ↩
いずれも二元数というものに分類されます ↩
この記事の本筋とは無関係ですが, 複素数も同様に行列表現ができます. $$ a + i b : \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}a + \begin{bmatrix} 0& -1\\ 1 &0 \end{bmatrix}b $$ この複素数の行列表現において $a = \cos\theta,\ b = \sin\theta$ とすると, 2次元の回転行列 $$ R(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{bmatrix} $$ が得られます. ↩
慣性座標系でボディ座標系の原点を並進移動してから, できあがったボディ座標系でボディ座標系を回転させる変換と等価 ↩
回転行列や同次変換行列と同じ要領で, 絶対変換は左から, 相対変換は右から掛けます. ↩
慣性座標系でボディ座標系を回転してから, できあがったボディ座標系でボディ座標系を並進移動する変換と等価 ↩
この式の導出をなんだかんだで見たことがないのですが, 単純に微分の定義とか回転行列の微分とかから出せるんですかね? ↩
これは, 単純計算により $\boldsymbol v^i$ を $\boldsymbol q_{ib}^\ast$ で回転させた $\boldsymbol q_{ib}^\ast \otimes \boldsymbol v^i \otimes \boldsymbol q_{ib}$ , つまり慣性座標系での並進速度を機体座標系でみたものと等しくなります. ↩
R.M. Murray, Z. Li, and S.S. Sastry, “A Mathematical Introduction to Robotic Manipulation”, 1994, CRC Press ↩
T.S. Andersen, T.A. Johansen, and R. Kristiansen, “Dual-quaternion backstepping control for a fully-actuated rigid-body”, 2018, American Control Conference ↩