概要
マイクロマウスと制御理論 の第2回めの記事です. 第1回では,マイクロマウスの典型的な構造である2輪台車の数学モデルの紹介と,壁トレース制御に関する考察を行いました.
2部にわけるということにしていましたが,今回書いてみたところ予想以上に内容が盛り沢山になってしまったため,3部に再編することにします. 今回の記事は,自由度と制御できる変数の数,劣駆動性と非ホロノミック拘束についてを主な内容として書いていきます. 次回,第3回の記事では,絶対運動と相対運動のどちらを制御するか(どの座標系に注目するか)による違いを書きたいと思います.
もくじ
- 非ホロノミック拘束 1.1 自由度 1.2 非ホロノミック拘束 1.3 2輪台車の非ホロノミック性
- まとめ
非ホロノミック拘束
非ホロノミック拘束という言葉を聞いてピンとくる方はマイクロマウスを作られている方にもあまりいらっしゃらないかもしれません. 非ホロノミック拘束は数学的には不可積分な微分拘束のことです.2輪台車が真横に動けないという拘束はこれの一種です.
自由度
非ホロノミックシステムとよく混同される概念として,劣駆動システムというものがあります.まずはこちらの概念に触れておきます.
その前に少しクイズを出しましょう.
Q1. 平面上を運動する剛体の位置・姿勢を表現しようとすると,独立な変数がいくつ必要でしょうか? 答えは下の図のようになり,3変数あれば表現できることがわかります.
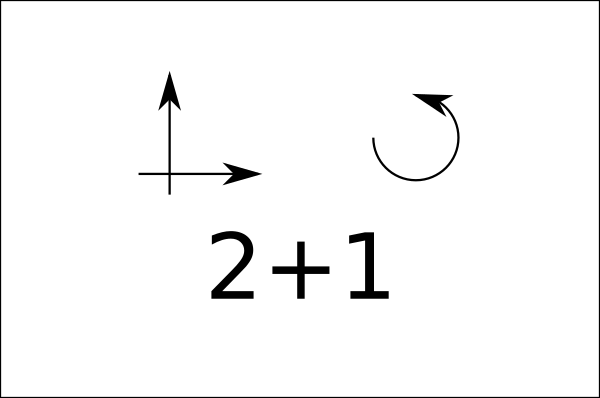
Q2. では3次元ではどうでしょう? 答えは下の図のようになり,6変数となります.
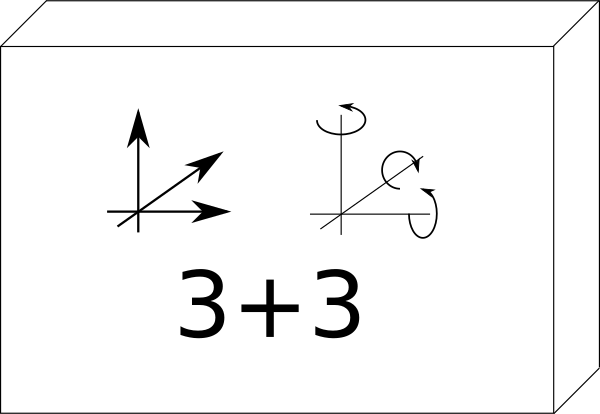
点の位置を決めるには \(x,y,z\) を取るか,角度2つと原点からの距離(球面座標)の計3変数があればよいのですが,ここでは点ではなく剛体の位置・姿勢を考えているため,変数としては6つになります.
Q3. つぎのような平面リンク機構だとどうでしょう? 答えは下図のとおりです.
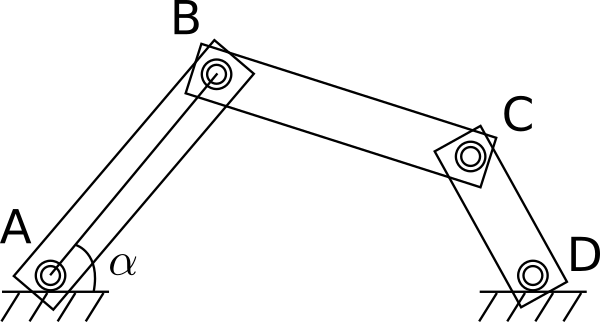
この例では,節 AB の姿勢が決まると BC と CD の姿勢も自動的に決まるので,変数の個数としては1となります.
このように,対象として考えるシステムの静的な状態(コンフィギュレーション, configuration)を表現するために必要な独立な変数の個数を 自由度 (degree of freedom, DoF) と呼びます. 独立な入力の数やアクチュエータの数を自由度として定義している場合がありますが(例えばRCサーボを使ったロボットとか),工学的には先述のような定義が使われます.
特に私たちがよく考える力学系において,自由度の概念はシステムの特徴を把握するのに使われます. 下の表は,独立な運動をつくる入力の数と自由度の関係による性質の違いを示したものです.
| 関係 | 性質 |
|---|---|
| (入力の数) < (自由度) | 劣駆動 underactuated |
| (入力の数) = (自由度) | 全駆動 fully-actuated |
| (入力の数) > (自由度) | 冗長 redundant, overactuated |
自由度が機体の独立な入力の個数より多い場合,すなわち劣駆動の場合は,(自由度)-(入力の数) 分の自由度は何らかの形で使えなくなります. 最近流行りのクアッドロータ(クアッドコプター,「ドローン」なんて呼ばれてたりもしますが…)がその好例です. クアッドロータは独立な 4つの入力 が4枚のプロペラによって生み出されますが,Q2 でも示したように3次元空間上での位置・姿勢の自由度は 6 です. したがってクアッドロータは劣駆動システムで,結果として機体を傾けなければ水平方向に加減速することができません.
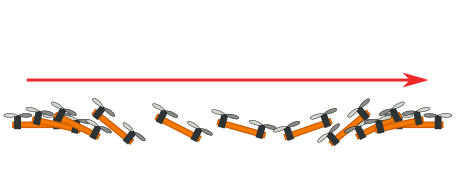
前半記事のモデルからも分かるように,2輪台車も機体の角度を変えないと横方向に動くことができません.そういう意味で,実はクアッドロータと2輪台車はよく似たシステムであると言えます.
非ホロノミック拘束
前節で述べたような使えなくなる自由度は,運動に対して課される拘束として考えることができます. この意味で,劣駆動なシステムは何かしらの拘束を受けながら運動をするわけです.
よく考えられる運動の拘束は次式のように表現されます. $$ A(q)\dot q = 0 $$ ただし,拘束の数を \(k\) 個とし, \(q \in Q \subset \mathbb{R}^n,\ A(q) \in \mathbb{R}^{k\times n}\) とします. このような形式で表現される拘束を Pfaff 拘束 (Pfaffian constraint) と呼びます. Pfaff 拘束は,特に力学系では速度 \(\dot q\) に対して課される拘束として考えることができます. この式は \(\mathrm{Ker}~A(q)\) (これを拘束の 零空間 と言います)の基底方向にしか動けないことを表していると解釈することができます. ここで重要なのは,動ける方向が位置・姿勢 \(q\) に対して \(A(q)\) という行列の形で決まるということです.
上記の Pfaff 拘束は速度に対する拘束を表すものでしたが,位置・姿勢に対する直接的な拘束を考えることもできます. $$ h(q)=0 $$ ただし,\(h: Q \rightarrow \mathbb{R}^k\) です.このような拘束を ホロノミック拘束 (Holonomic constraint) と呼びます. これを時間微分すると $$ \frac{\partial h(q)}{\partial q} \dot q=0 $$ となり,Pfaff 拘束の形式になります. しかし,逆は常には成り立ちません.すべての Pfaff 拘束がホロノミック拘束の形で表現できるとは限らないのです. $$ A(q)\dot q = 0 \Leftrightarrow \frac{\partial h(q)}{\partial q} \dot q=0 $$ となるような \(h(q)\) が存在するとき,この Pfaff 拘束は 可積分である といいます.そして,可積分でない (不可積分な) Pfaff 拘束は 非ホロノミック拘束 (Nonholonomic constraint) の一種です. 非ホロノミック拘束自体の定義は別にあるのですが,混乱を生みそうなので,以降は 非ホロノミックな Pfaff 拘束 について考えることにします.
2輪台車の非ホロノミック性
さて,ここまでの話を2輪台車システムに適用してみましょう.
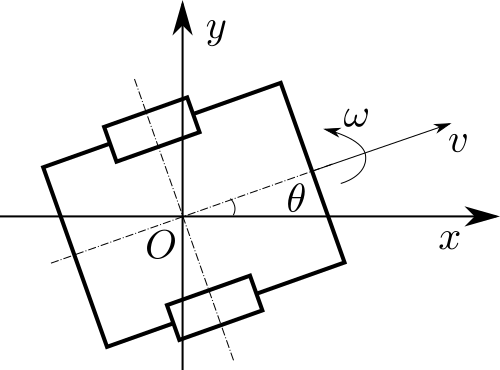
ロボットの状態を \(q = \left[ x\ y\ \theta \right]^T \),入力を \(u = \left[ v\ \omega \right]^T\) とすると, $$ \dot q = \begin{bmatrix} v\cos\theta\\ v\sin\theta\\ \omega \end{bmatrix} = \begin{bmatrix} \cos\theta & 0\\ \sin\theta & 0\\ 0 & 1 \end{bmatrix} u $$ なる状態方程式を使って2輪台車の運動を表現できることを前半の記事で示しました.
これをもとに真横に動けないという速度拘束を式で表すとつぎのようになります. $$ \begin{bmatrix} \sin\theta & -\cos\theta & 0 \end{bmatrix} \begin{bmatrix} \dot x\\ \dot y\\ \dot \theta \end{bmatrix} = \dot x\sin\theta - \dot y\cos\theta = 0 $$ この拘束が可積分かどうかを調べれば良いわけですが,その方法(Frobeniusの定理を使います)については今回は割愛します. 結論からいうとこの拘束は不可積分で,2輪台車は非ホロノミック拘束を受ける非ホロノミックシステムです.
Brockettの定理
Brockettの定理は,非線形システムの可制御性に関する有名な定理です(詳しくは参考文献 3 を参照). この定理によると,非ホロノミック拘束をもつ(かつ定理の条件を満たす)システムは静的連続状態フィードバックでは漸近安定化(状態をすべて0に収束させること)が不可能であるという衝撃的な結論が得られます. 静的状態フィードバックとは,例えば線形の制御則でいうとPD制御やLQ最適制御のような,状態変数の値から入力が一意に決まるようなフィードバック制御則です.
特に2輪車両についてくだけた言い方をすると,2輪台車は普通の方法で位置・姿勢を同時に制御するのが困難だということになります. この嫌な状況をかいくぐるための方策として提案されてきたものとして,以下の3つの戦略が代表的です.
- 時変状態フィードバックを導入する
- 不連続フィードバックを導入する
- 時間軸を曲げる(時間軸状態制御系を使用する)
この辺の話については参考文献 4 にたいへん詳細に書かれていますので,興味のある方は参照してみてください.
さて,マイクロマウスを作って制御する人にとって気になるのは,「ではなぜみなさん当たり前のようにマイクロマウスが走っているのか」ということになると思います. 実は,マイクロマウスの動作に限定して言えば上述したような困難は緩和されます.という話を次回の記事で書こうと思います.
まとめ
- 空間・機構の自由度についてざっくり解説をした
- Pfaff拘束とその可積分性,非ホロノミック拘束について説明した
- 2輪台車が非ホロノミックシステムであることを示した
- Brockettの定理に触れ,2輪台車が位置姿勢を同時に制御しづらいシステムであることを説明した
次回は今回の内容を前提として,絶対運動の制御(慣性座標系での制御)と相対運動の制御(機体座標系での制御)を行う際に現れる違いについて,理論面と実用面から書きます.
参考文献
- 美多 勉, “非線形制御入門―劣駆動ロボットの技能制御論” (※絶版). 昭晃堂, 2000.
- R. Murray, S. Sastry and Z. Li, “A Mathematical Introduction to Robotic Manipulation”. CRC Press, 1994.
- R. Brockett, R. Millman and H. Sussman, "Differential Geometric Control Theory”. Springer Verlag, 1983, pp. 181–208.
- 三平 満司, 石川 将人, 非ホロノミックDriftlessシステムのフィードバック制御.