概要

これは rogy Advent Calendar 2018 3日目の記事です. 投稿時点で12/3の25時ですが許して.

3次元回転は, 航空機, 人工衛星, マルチコプターなどの姿勢制御や, 3DCG, VR/AR, コンピュータビジョンなど, 3次元の物体が関わるあらゆる技術に密接に関係しています. この強力なツールを習得すればできることがぐっと増えるのですが, 回転の順序を入れ替えられないことや, 回転の基準とする座標系の取り方によって結果が変わること, 数学的な表現が初学者には分かりづらいことなどを理由に, 敬遠されがちなのが実情です. 実際, わたしも特に座標系にはさんざん苦しめられながら学習してきた経緯があり, 研究で取り扱っている今でもたまに混乱することがあるほどです.

これから書いていくシリーズ「たのしい3次元回転の世界」では, 3次元の回転に関わる事実や諸注意をなるべく図的に解説し, 扱う際の混乱や誤解をなくすことを目標にしています. 特にクォータニオンに関しては, 「なぜこれで回転が表現できるのかわからない」「イメージがしづらい」という意見をよく目にしますので, そのあたりに関する解釈も書いていければと思います. 筆者は数学的な深い知識には乏しい人間ですので, あまり数学的に立ち入った内容にはせず, 読み物としてためになるものが書ければと考えています. したがって, 数学的にプロパーな解説は, ほかの方の記事や論文等を参照していただくのが良いと思います.

今回は 3次元回転の特徴 について記します. 3次元空間内の回転は, 2次元平面上での回転にない特徴を多くもっています. まずはその特徴に触れることで, 3次元の回転へのイメージを養うことからこのシリーズをはじめたいと思います.

3次元の回転と姿勢

2次元平面上の回転が1つのパラメータで表されるのに対して, 3次元空間内の回転は少なくとも3つのパラメータを用いて表現します.

任意の3次元の回転操作は, 3x3の回転行列で表すことができます. 回転行列は, 3次元の姿勢を表すためにも使うことができます. 基準となる座標系をゼロ回転(単位行列)とすれば, そこからの回転操作で姿勢を考えることができるからです.

このシリーズでは, 特にことわりがない限り $R$ を回転行列として扱います.

座標系

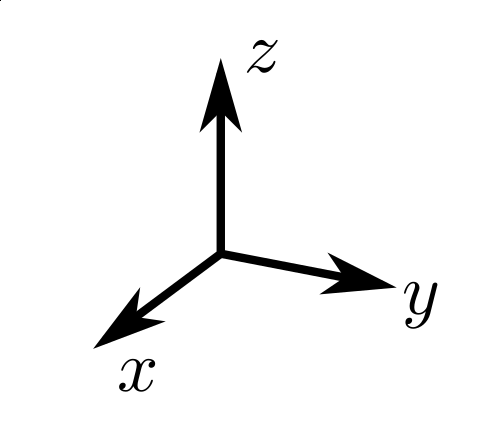
座標系とは, 雑に説明すると, 「こっちが上」「こっちが右」みたいな印を数学的に記述したものです. 3次元の座標系は, ふつう $x, y, z$ という3つの直交する軸の組を使って表現します.

座標系は3次元空間内に異なるものを複数もつことができます. たとえば, 地面に固定した座標系を考えても良いし, 地面を走ったり空中を飛んだりするロボットに取り付けた座標系を考えても良いわけです. これらはそれぞれ異なる姿勢をもつ座標系になり, それぞれの座標系によって $x, y, z$ 軸の指す方向が異なります.

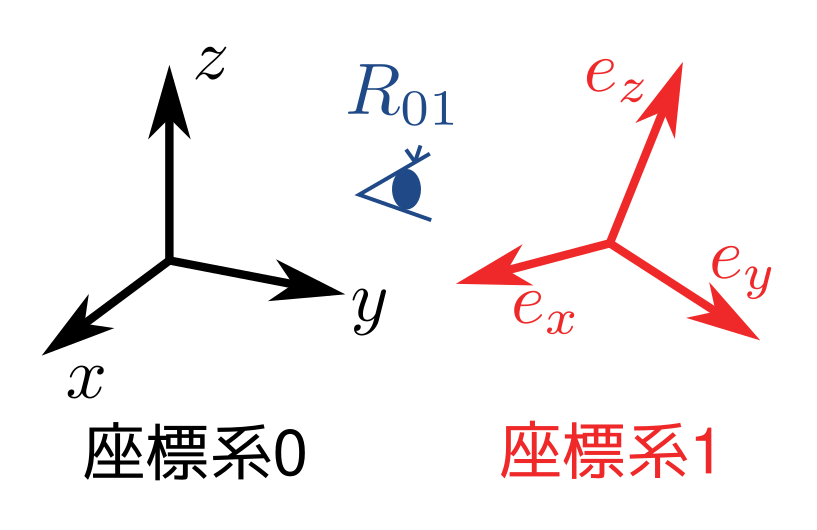
上図の座標系1の軸を座標系0で表現した方向ベクトル $e_x, e_y, e_z$ を横に並べて行列を作ると, これは回転行列になります. $$ R_{01} = \left[ e_x\ e_y\ e_z \right] $$ $R_{01}$ は, 座標系0 から見た 座標系1 の姿勢 を表す回転行列, というふうに読みます.

回転行列を使うと, 2つの座標系の間の姿勢の関係を表すことができるようになります. 座標系0を地面に固定した座標系, 座標系1をロボットに取り付けた座標系と考えると, 地面から見たロボットの姿勢が $R_{01}$ で表されることになります. わかりにくければ $R_{地面,ロボット}$ などと書いてもおっけーです.

本来3次元空間内の座標系というと, 原点の位置も3次元空間内で自由に選べるのですが, このシリーズでは回転だけを考えるので, すべての座標系の原点は同一の点Oを用いることにします. また, 座標系0は動かない座標系を表すことにします.

回転行列によるベクトルの回転

先述の回転行列 $R_{01}$ は, 座標系1で表現されたベクトル $p_1$ を座標系0での表現に変換する役割を果たします. $$ p_0 = R_{01}p_1 $$ このように, 添字をぷよぷよ式に消すような表現にしておくと便利です.

回転の合成

回転行列を掛け合わせることによって, 3次元の回転を合成することができます. $$ R_{02} = R_{01}R_{12} $$ 一般に, この計算の順序は入れ替えることはできません. これについては次節で詳しく述べます.

3次元の回転はややこしい

紙面方向しか回転軸がない2次元平面上の回転とは異なり, 3次元空間内の回転は, 軸の選び方に大きな自由度があります. これに起因して, 3次元の回転にはとにかくややこしい性質がいくつもつきまといます.

本節では, 代表的な性質を3つ紹介します.

• 順序を入れ替えられない
• 回転の基準とする座標系の選び方によって結果が変わる
• 角速度の単純な時間積分は姿勢角にならない

順序を入れ替えられない (非可換性)

だんだん疲れてきたと思うので, 少し体操をして目を覚ましましょう. ふつうに体操をするだけではつまらないので, 3次元の回転に思いを馳せながらやってみることにします. かわいいゆかりさんにお手本を見せてもらいましょう.

まず片手を前に出して, 手のひらが横を向くようにしてください.

この状態から, 親指方向に90度回して手を上に上げてください.

つぎに, 手の甲の方向に90度回して, 手を横に出します.

最後に, 小指方向に90度回して, 手を前に戻します.

この3つの回転によって, 最終的に手のひらが上向きで前に出た状態になります.

---

今度はこの手順を逆にしてやってみましょう. もう一度最初の状態に戻します.

今度は, はじめに小指方向に90度回して手を下に下げてください.

つぎに, 手の甲の方向に90度回して, 手を横に出します.

最後に, 親指方向に90度回して, 手を前に戻します.

今度は手のひらが下を向いています.

あれ, 回転の操作の順序を変えただけなのに, 最終的な結果が変わってしまいました. この事実は, 行列の非可換性という性質の表われです. $$ R_{02} = R_{01}R_{12} \neq R_{12}R_{01} $$ 同じ軸まわりの回転であれば, 隣同士の順序を入れ替えても問題ありませんが, それ以外の場合は結果の姿勢が異なるものになります.

ちなみに2次元平面上の回転の場合は, 回転軸が平面に垂直な方向の1つしか存在し得ないのでこのようなことは起こらず, 最初に右回りに回しても左回りに回しても最終的に同じ結果が得られます. むしろ2次元平面上の回転の方が特殊だということに気づいていただければと思います.

回転の基準とする座標系の選び方によって結果が変わる (絶対変換と相対変換)

先ほどの例では, 手の指の向きを基準にした手の回転を行っていました. 今度は, 顔の向きを基準にして同様に手を回してみようと思います.

まずはじめに, 先ほどの最初の状態と同様に片手を前に出して, 手のひらが横を向くようにしてください. この状態で, 顔の向きと手の向きの対応関係を取ります.

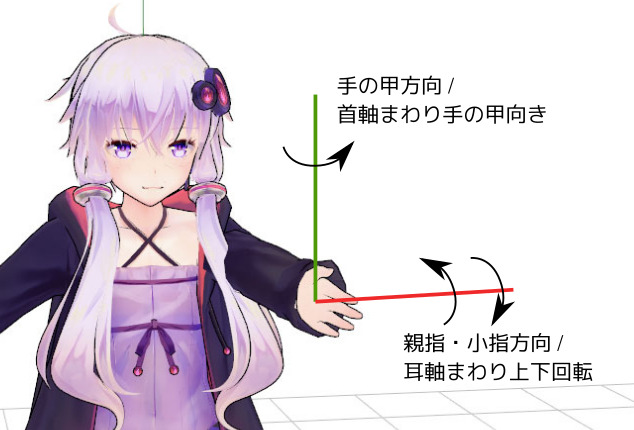
手の向き基準	顔の向き基準
親指方向への回転	頭頂方向への耳軸まわりの回転
小指方向への回転	あご方向への耳軸まわりの回転
手の甲方向への回転	もともと手の甲が向いていた方向への首軸まわりの回転

ちょっとややこしいですがご容赦ください.

---

では回していきましょう. この状態から, 小指方向に対応するように, 耳軸まわりにあご方向へ90度回します.

つぎに, もともと手の甲が向いていた方向に首軸まわりに90度回します. 手をひねるような動作になります.

最後に, 耳軸まわり頭頂方向に90度回します. 手を元の位置に戻してくるような動作になります.

さて, やってみて気づくことがありませんか? 鋭い方はお気づきかもしれませんが, 顔の向きを基準に回転を行うと, その逆順で手の向きを基準に回転を行った際と同じ結果になります. これはほかの回転パターンでも常に成り立ちます.

回転する物体(手)を基準にする場合と, 動かない物体(顔)を基準にする場合にはこのような関係があります.

実は, どちらの回転も数式で表現すると $$ R_{03} = R_{01} R_{12} R_{23} $$ という全く同じ回転行列の積で表現することができます.

より一般的には, 行列を左右どちらからかけ合わせるかによって, 回転の基準とする座標系を以下のように選ぶことができます. もとの姿勢を $R$, 与える変換を $R_\mathrm{trans}$ とします.

左からかける場合(絶対変換) $$ R_{\mathrm{abs}} = \color{red}{R_\mathrm{trans}} R $$ この操作は, 顔の向き(動かない座標系)を基準にした回転操作に対応します.

右からかける場合(相対変換) $$ R_{\mathrm{rel}} = R \color{red}{R_\mathrm{trans}} $$ この操作は, 手の向き(動かした後の座標系)を基準にした回転操作に対応します.

先ほどの例ですと, $$ \begin{align*} \underbrace{R_{03}}_{\text{初期状態からみた終端状態の姿勢}} &= \underbrace{R_{01}}_{\text{親指方向}}\ \underbrace{R_{12}}_{\text{手の甲方向}}\ \underbrace{R_{23}}_{\text{小指方向}}\\ &= \underbrace{R_{01}}_{\text{耳軸まわり上方向}}\ \underbrace{R_{12}}_{\text{首軸手の甲方向}}\ \underbrace{R_{23}}_{\text{耳軸まわり下方向}}\\ \end{align*} $$ のように対応しています.

角速度の単純な時間積分は姿勢角にならない

先ほどの腕の回転の順序を変える例を考えると, どちらの場合も親指方向の変化量の積算値は 90-90 で 0 度, 手の甲方向は 90 度になります. この例から, 結果として異なる姿勢が得られるにもかかわらず, 同じ積算値(角速度の積分値)となる場合があるということがわかります. つまり, 角速度を単純に時間積分した数値を見ても, 物体が今どのような姿勢になっているかということは知ることができないのです.

このことは, 姿勢の時間変化がそのときの姿勢に大きく依存していることに起因しています. 実際, 回転行列の時間微分 $\dot{R}$ は以下のような式になります. $$ \dot{R} = R \widehat\omega $$ ただし, $$ \widehat\omega = \begin{bmatrix} 0 & -\omega_3 & \omega_2\\ \omega_3 & 0 & -\omega_1\\ -\omega_2 & \omega_1 & 0 \end{bmatrix} $$

まとめと次回予告

今回は, 3次元の回転にまつわる性質について紹介しました. 我々はこんなややこしい空間に住んでいて, しかも何も考えずにものの姿勢をいじれるって, なかなか驚きですよね.

書いたことをまとめると, 以下のとおりです.

• 3x3回転行列は3次元の姿勢の表現でもあり, 3次元の回転操作を表すものでもある
• 座標系0からみた座標系1の姿勢を表す回転行列は, 座標系1のベクトルを座標系0に移すはたらきをする
• 3次元の回転は, 順序を入れ替えられない
• 3次元の回転は, 回る座標系を基準にするか回らない座標系を基準にするかによって異なる
• 角速度ベクトルを単純に積分しても, 姿勢角は得られない

次回は

• オイラー角とクォータニオン
• なぜオイラー角はクソでクォータニオンは便利なのか
• クォータニオンの幾何的な考え方 の3本をお送りしたいと考えています. 12/8頃公開予定.